皆様こんにちは,同志社大学の土屋誠司です.人工知能の第29回目の今回は,クラスタリングについて書いてみたいと思います.
クラスタリングとは,物事をいくつかのカテゴリ(クラスタ)に分類する処理のことです.最も基本的で単純な手法として,k近傍法(k-NN(Nearest Neighbor)法)があります.あらかじめクラスタの個数をk個と決め,k個のクラスタの代表を作っておきます.そして,このk個のクラスタの代表に近いものを同じクラスタとします.図1では,黒い丸やグレーの丸が代表を表しています.ここでポイントは,分類したいものをしっかりと観察して,適切にk個のクラスタの代表を決めてやる必要があるということです.

図1 k近傍法のイメージ図
しかし,k個のクラスタの代表を適切に決めることは一苦労です.そこで,別の方法として,k平均法(k-means法)があります.この方法は,先ほどのk近傍法とよく似ています.まず,あらかじめクラスタの個数をk個と決めておき,k個の代表を作っておきます.図2の左の図では黒い×印が代表を表しています.そして,このk個の代表に近いものを同じクラスタとします.ここまでは,k近傍法と同じです.
違いはここからです.同じクラスタになったものから,そのクラスタの中心を計算し,代表をその中心に置き換えます.図2の真ん中の図の白い×印が元の代表,黒い×印が新しく計算した中心です.各クラスタの中心が移動しなくなるまでこの作業を繰り返すことで,図2の右の図のように,最終的にk個のクラスタを作ることができます.なお,クラスタの良し悪しは,初めに決めるk個の代表に大きく依存するため,なるべく離れるようにk個の代表を決めること,また,複数回実行するなどの工夫が必要となります.そうすることで,良いクラスタになることが期待できます.
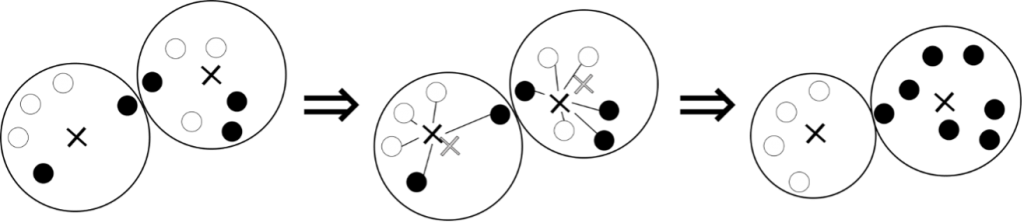
図2 k平均法のイメージ図
その他には,階層型クラスタリングというものがあります.これは,近いもの同士をペアにして行き,そのペアにする過程を階層構造として整理します.階層構造となる結果は,図3のように,デンドログラムと呼ばれるトーナメント表のような木構造の形式で表現できます.この方法では,任意の個数のクラスタに分類することができます.
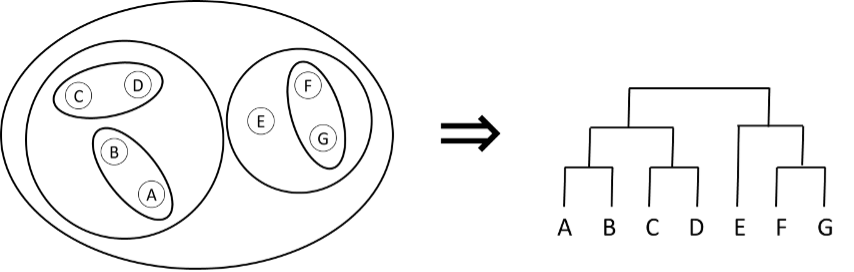
図3 階層型クラスタリングのイメージ図
次回は,引き続き,物事を分類するクラスタリング手法として,有名でもう少し難しいやり方であるサポートベクターマシン(SVM)について書いてみたいと思います.

